Secara
lebih visual, gejala chaos pertama kali dipelajari secara tidak sengaja
oleh Edward N. Lorenz, seorang pakar sains atmosfir dari MIT, di tahun
1963. Kala itu ia tengah mencoba memodelkan aliran konveksi udara tiga
dimensi di atmosfir. Lorenz menurunkan model ideal persamaan nonlinier
yang terkopel tiga dan berusaha memecahkannya secara numerik
menggunakan pertolongan komputer. Alih-alih memperoleh pemecahan yang
berkelakuan baik, ia malah menemukan perilaku aneh yang semula ia
anggap sebagai kesalahan numerik. Hasil yang diperoleh menunjukkan
bahwa lintasan pemecahan dalam ruang tiga dimensi tersebut memiliki
ciri lintasan yang tidak teratur.(strange attractor), dan tidak
pernah menempuh lintasan yang sama. Jika titik awal perhitungan
dirubah sedikit saja, maka akan muncul pola orbit dengan kelakuan serupa
tetapi memiliki pola lintasan yang lain sama sekali.
Hingga
kini, gejala chaos juga dapat dijumpai dimana-mana, mulai dari sistem
fisika seperti sirkuit listrik, turbulensi gerak benda dalam fluida,
fenomena superkonduktor, gerak bandul, sistem jaringan syaraf, atau pada
perubahan cuaca. Pemodelan mengenai perilaku sistem sosial, fluktuasi
harga saham, dan pola hubungan antara mangsa dan pemangsa di dalam suatu
ekosistem pun memprediksikan kemungkinan munculnya chaos.
Sistem
Lorenz adalah sistem autonomous yang sederhana dengan tiga persamaan
diferensial biasa terkopel yang bersifat nonlinier. Sistem Lorenz
pertama kali diperkenalkan oleh Edward N. Lorenz (1963) ketika membuat
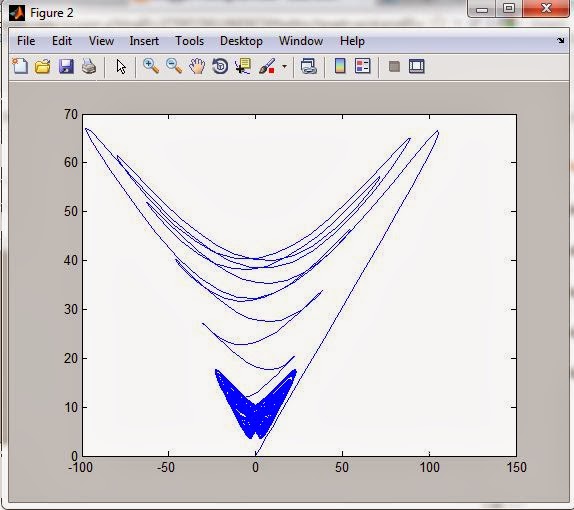
model matematika dari konveksi tiga dimensi di atmosfer Hasil Matlab
untuk persamaan sirkuit Lorenz adalah sebagai berikut:
Dalam
karya ini sistem New Lorenz-Like, disajikan oleh Li dkk pada tahun 2008
[2], digunakan. istem nonlinier auotonomous tiga dimensi yang
digambarkan oleh sistem persamaan diferensial biasa di bawah ini.
Dimana
adalah variable keadaan dari sebuah sistem. a, b, c adalah parameter dari
sebuah sistem. Seperti yang ditunjukkan pada persamaan (1) sistem persamaan
diferensial, tetapi non-linier sistem hanya bergantung pada istilah dua kuadrat
xy dan xz.
Dalam
Gambar di atas, proyeksi orbit ruang fase ke bidang xy, bidang xz dan bidang
yz, ditunjukkan masing-masing. Parameter dan kondisi awal dari New Lorenz-Like
sistem (1) adalah (a, b, c) = (5, 4, 2.5) dan (x0, y0, z0) = (0,1, 0,1, 0,1),
sehingga sistem menunjukkan perilaku chaos yang diharapkan. Jadi, dapat dilihat
dengan jelas bahwa potret fase, terutama pada bidang xz mirip dengan yang ada
pada sistem Lorenz.
Sebuah
skema rangkaian yang berhubungan dengan sistem Lorenz ditunjukkan pada
Gambar di atas. Tegangan pada node berlabel x, y, z dan sesuai dengan
kedaan dari sistem persamaan (1). Penguat operasional dan sirkuit
terkait menunjukkan operasi dasar penambahan, pengurangan, dan
integrator. Istilah nonlinier dalam persamaan ditunjukkan dengan analog
pengganda AD633 [2]. Terjadinya attractor chaos dapat terlihat jelas
pada Gambar di bawah ini dengan menggunakan Multisim 10.0.
 09.03
09.03
 fisikawan muslim
fisikawan muslim